La paradoja de Bertrand.............................. Carlo Frabetti.

Cuando se juntan el azar y el infinito, los resultados pueden ser desconcertantes.

Joseph Bertrand.

Con motivo de la entrega número 200 de El juego de la ciencia, nos preguntábamos la semana pasada si cambiando una cifra de este número tan redondo y “excesivo” podemos convertirlo en primo. 
Y la respuesta es no. 
Evidentemente, la cifra a cambiar tiene que ser la de las unidades, pues un número terminado en 0 es divisible por 10, y esa última cifra no puede ser par, y tampoco puede ser 1, 5 ni 7, pues si la suma de las cifras de un número es divisible por 3, lo es el propio número.
 Los únicos candidatos son 203 y 209; pero 203 es divisible por 7, y 209 es divisible por 11; por lo tanto, no se puede convertir 200 en primo cambiando una de sus cifras.
 Y, por cierto, 200 es el menor número con esta propiedad.

 

En cuanto a la secuencia 2, 10, 12, 16, 17, 18, 19, 200…, es la de los números cuyo nombre empieza por la letra d.

El infinito y el azar

Todos tenemos -o creemos tener- una idea intuitiva de lo que es el azar, y también sabemos que hay infinitos números y que en una recta hay infinitos puntos. Pero cuando intentamos operar con estos escurridizos conceptos y llegar a conclusiones claras, nos encontramos a menudo con desconcertantes paradojas.
Una de las más famosas es la paradoja de Bertrand, denominada así en honor del matemático francés Joseph Bertrand, que la expuso a finales del siglo XIX en su ya clásico Calcul des probabilités.
Para ilustrar su paradoja, Bertrand utilizó un ejemplo que los lectores sacaron a relucir la semana pasada y que dio lugar a un animado e interesante debate (ver comentarios de “El número 200”). El ejemplo es el siguiente:

¿Cuál es la probabilidad de que una cuerda trazada al azar en una circunferencia sea mayor que el lado del triángulo equilátero inscrito en ella?

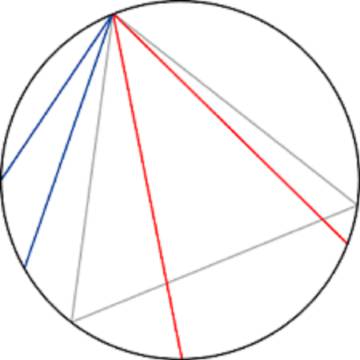
Las cuerdas de todas las longitudes posibles pueden partir de un mismo punto cualquiera, puesto que todos los puntos de la circunferencia son equivalentes; consideraremos, pues, que uno de los extremos de la cuerda es uno de los vértices del triángulo equilátero inscrito;
 si la cuerda cae dentro del triángulo, su longitud será mayor que el lado del mismo, y si cae fuera será menor, y como el ángulo del triángulo equilátero es de 60º y todas las cuerdas posibles abarcan un ángulo de 180º (pues el límite está en la tangente a la circunferencia en el vértice que hemos tomado como origen), la probabilidad pedida será 60/180 = 1/3. Un razonamiento impecable; pero…
Consideremos ahora un radio perpendicular a un lado del triángulo inscrito.
 Todas las cuerdas perpendiculares a dicho radio que quedan entre el centro de la circunferencia y el lado del triángulo son mayores que él, y todas las que quedan entre el lado y el otro extremo del radio son inferiores.
 Y como el lado del triángulo equilátero inscrito divide al radio en dos partes iguales, la probabilidad pedida será 1/2.
Y aún hay otro criterio que nos da una probabilidad de 1/4, y todos los planteamientos parecen válidos.
 Invito a mis sagaces lectores/as a reflexionar sobre esta desconcertante paradoja y a proponer otros ejemplos de probabilidades paradójicas o sorprendentes.
 Como este:
Si trazamos una circunferencia al azar en una hoja de papel cuadriculado, ¿cuál es la probabilidad de que pase por alguno de los puntos de intersección de la cuadrícula?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.